二叉树 & 二叉查找树 ADT【数据结构与算法分析 c 语言描述】

1. 引言

主要涉及知识点

二叉树的概念。
二叉查找树的概念跟常用操作。
二叉树的遍历（先序遍历、中序遍历、后序遍历、层序遍历）。

其他

队列（层序遍历用到）。

最后留了两个思考的点

delete 为什么要 return t。
为什么是 t->right = delete(x, t->right) 而不直接 delete(x, t->right)。

2. 概念

树是一种非线性数据格式，计算机里面非常有用的数据格式之一，最常用的其中就有二叉树、二叉查找树，

二叉树：每个节点都不能有多余两个儿子的一棵树二叉查找树：对于树种的每一个节点 X ，都满足它的左子树的关键字小于 X 的关键字，右子树的关键字大于 X 的关键字并且 X 的关键字是不重复的。

二叉查找树是基础性数据结构，用于构建更为抽象的数据结构，如集合、multiset、关联数组等，二叉树的优点是插入、查找时间复杂度低 O(logN)。

3. 二叉查找树的思路

定义一颗二叉查找树的结构体

typedef struct tree_node
{
    element_type element; //节点关键字
    struct tree_node *left; //左子树
    struct tree_node *right; //右子树
} *search_tree;
typedef search_tree position;

一棵标准二叉查找树需要实现的方法

search_tree make_empty(search_tree t);
position find(element_type x, search_tree t);
position find_min(search_tree t);
position find_max(search_tree t);
search_tree insert(element_type x, search_tree t);
search_tree delete(element_type x, search_tree t);
element_type retrieve(position p); //检索值

麻烦一点儿的在删除。删除的节点有三种情况：

是树叶——直接 delete。
有一个儿子：父节点直接指向子节点。
有两个儿子：右子树最小的数据代替该节点，并删除那个节点（右子树最小节点、直接递归删）。

4. 二叉树遍历

先序遍历：root 节点->左节点->右节点。
中序遍历：左节点->root 节点->右节点。
后序遍历：左节点->右节点->root 节点。
层序遍历：逐层遍历。重点说层序遍历。

5. 具体实现

queue.h头文件，就是一个队列，具体实现代码参照队列那篇文章

#include <stdio.h>
#include <stdlib.h>
#include "bitree.h"

#define error(str) fatal_error(str)
#define fatal_error(str) fprintf(stderr, "%s\n", str),exit(1)

struct node;
typedef search_tree queue_element_type;
typedef struct node *ptr_to_node;
typedef ptr_to_node queue;

queue create_queue();
void queue_make_empty(queue q);
int is_empty(queue q);
void enqueue(queue_element_type x, queue q);
void dequeue(queue q);
queue_element_type front(queue q);
queue_element_type front_and_dequeue(queue q);
void dispose_queue(queue *q);

bitree.c 文件

/**
 * 二叉查找树
 */

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include "queue.h"
#include "bitree.h"

struct tree_node
{
    element_type element; //节点关键字
    struct tree_node *left; //左子树
    struct tree_node *right; //右子树
};

search_tree make_empty(search_tree t)
{
    if (NULL != t) {
        make_empty(t->left);
        make_empty(t->right);
        free(t);
    }
    return NULL;
}

position find(element_type x, search_tree t)
{
    if (NULL == t)
        return NULL;

    if (t->element > x)
        return find(x, t->left);
    else if(t->element < x)
        return find(x, t->right);
    else
        return t;
}

position find_min(search_tree t)
{
    /*非递归*/
    /*if (NULL != t)
        while (t->left != NULL)
            t = t->left;
    return t;*/
    //递归
    if (NULL == t)
        return NULL;

    if (NULL == t->left)
        return t;
    else
        return find_min(t->left);
}

position find_max(search_tree t)
{
    /*递归*/
    /*if (NULL == t)
        return NULL;

    if (NULL == t->right)
        return t;
    else
        return find_max(t->right);*/
    /*非递归*/
    if (NULL != t)
        while (t->right != NULL)
            t = t->right;
    return t;
}

search_tree insert(element_type x, search_tree t)
{
    if (NULL == t) {
        t = (search_tree)malloc(sizeof(struct tree_node));
        if (NULL == t)
            fatal_error("out of space");
        else {
            t->element = x;
            t->left = t->right = NULL;
        }
    } else if (x < t->element) {
        t->left = insert(x, t->left);
    }
    else if (x > t->element) {
        t->right = insert(x, t->right);
    }
    return t;
}

search_tree delete(element_type x, search_tree t)
{
    position temp_cell;
    if ( NULL == t)
        error("empty tree");
    else if(x < t->element) 
        t->left = delete(x, t->left);
        // delete(x, t->left); /*思考:为什么不直接 delete*/
    else if (x > t->element)
        t->right = delete(x, t->right);
        // delete(x, t->right); /*思考:为什么不直接 delete*/
    else if (t->left && t->right) { // 有两个儿子 找右子树最小节点
        temp_cell = find_min(t->right);
        t->element = temp_cell->element; // 右子树最小关键字替换上来
        // delete right child
        delete(temp_cell->element, t->right);
    } else { // 一个 or 0 个节点,不左还是右都是直接跨过 t 直接指向该节点
        temp_cell = t;
        if (t->left == NULL)
            t = t->right;
        else if (t->right == NULL)
            t = t->left;
        free(temp_cell);
        temp_cell = NULL;
    }
    return t; //是何用意?
}

element_type retrieve(position p)
{
    return p->element;
}


void print_tree(search_tree t, int type)
{
    if (NULL == t) {
        fatal_error("empty tree");
    }
    // 先序遍历
    if (type == 1)
        printf("%d ", t->element);

    if (t->left)
        print_tree(t->left, type);
    // 中序遍历
    if (type == 2)
        printf("%d ", t->element);

    if (t->right)
        print_tree(t->right, type);
    // 后序遍历
    if (type == 3)
        printf("%d ", t->element);
}

void print_layer(search_tree t)
{
    queue q;
    position p;
    q = create_queue();
    enqueue(t, q);
    while (is_empty(q) != 1) {
        p = front(q);
        printf("%d ", p->element);
        if (NULL != p->left)
            enqueue(p->left, q);
        if (NULL != p->right)
            enqueue(p->right, q);
        dequeue(q);
    }
}

void test()
{
    search_tree t;
    int i, x;
    t = make_empty(NULL);
    srand( (unsigned)time(NULL) );
    for( i = 0; i < 10; i++ )
        t = insert(rand() % 50, t);
    printf("\n先序遍历:");
    print_tree(t, 1);
    printf("\n中序遍历:");
    print_tree(t, 2);
    printf("\n后序遍历:");
    print_tree(t, 3);
    printf("\n层次遍历:");
    print_layer(t);
    printf("\n");
    printf("max：%d\n", find_max(t)->element);
    printf("min：%d\n", find_min(t)->element);
}

int main(int argc, char const *argv[])
{
    test();
    return 0;
}

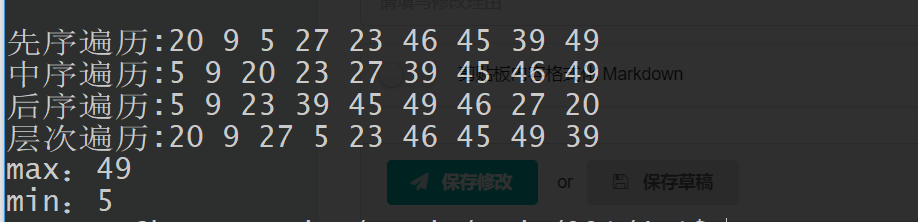
7. 运行截图

file