ps:我怕我发的会打扰到大家,本意只是想记下学习研究过程跟结果,这些很基础的东西,如果打扰到大家的话在底下说下,以后就不发这种了
/**
* 给定(可能有负数)整数a(1)、a(2)、……a(n),求 a(1)+a(2)+……+a(j)的最大值。
* 为方便起见,若所有的整数为负数,则最大子序列和为0.
* 描述:在一系列整数中,找出连续的若干个整数,这若干个整数之和 最大。
*
* 四个算法,充分体现出优秀的算法的重要性
*/
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
// #define N 100
int bigO_n3(int arr[], int n);
int bigO_n2(int arr[], int n);
int bigO_logn(int arr[], int left, int right);
int bigO_n(int arr[], int n);
// 第三个算法用到
int max(int a, int b, int c);
int main(void)
{
int * arr;
clock_t elapse;
printf("\t\tO(n^3)\t\tO(n^2)\t\tO(logn)\t\tO(n)\n");
printf("\tN\t耗时\t\t耗时\t\t耗时\t\t耗时\n");
for (int N = 10; N <= 10000; N = N*2) {
srand((unsigned)time(NULL));
arr = (int *) malloc(sizeof(int) * N);
for (int j = 0; j < N; j++) {
arr[j] = rand() % 2001 - 1000;
}
printf("\t%d", N);
elapse = clock();
bigO_n3(arr, N);
elapse = clock() - elapse;
printf("\t%.6lf", (double) elapse / CLOCKS_PER_SEC );
elapse = clock();
bigO_n2(arr, N);
elapse = clock() - elapse;
printf("\t%.6lf", (double) elapse / CLOCKS_PER_SEC );
elapse = clock();
bigO_logn(arr, 0, N - 1);
elapse = clock() - elapse;
printf("\t%.6lf", (double) elapse / CLOCKS_PER_SEC );
elapse = clock();
bigO_n(arr, N);
elapse = clock() - elapse;
printf("\t%.6lf", (double) elapse / CLOCKS_PER_SEC );
printf("\n");
free(arr);
}
// bigO_n3()
return 0;
}
int bigO_n3(int arr[], int n)
{
int currenSum, maxSum, i, j, k;
maxSum = 0;
for (i = 0; i < n; i++) {
for(j = i; j < n; j++) {
currenSum = 0;
for (k = i; k <= j; k++)
currenSum += arr[k];
if (currenSum > maxSum)
maxSum = currenSum;
}
}
return maxSum;
}
int bigO_n2(int arr[], int n)
{
int currenSum, maxSum, i, j;
maxSum = 0;
for (i = 0; i< n; i++) {
currenSum = 0;
for( j = i; j < n; j++) {
currenSum += arr[j];
if (currenSum > maxSum)
maxSum = currenSum;
}
}
return maxSum;
}
int bigO_logn(int arr[], int left, int right)
{
int currenSum, maxSum, j, center;
int leftBorderSum, rightBorderSum;
int maxLeftBorderSum, maxRightBorderSum;
int maxLeftSum, maxRightSum;
// 单个数
if ( left == right) {
if (arr[left] > 0)
return arr[left];
return 0;
}
//分
center = (int)(left + right) / 2;
//最大值
maxLeftSum = bigO_logn(arr, left, center);
maxRightSum = bigO_logn(arr, center + 1, right);
maxLeftBorderSum = 0; leftBorderSum = 0;
for (j = center; j >= 0; j--) {
leftBorderSum += arr[j];
if (leftBorderSum > maxLeftBorderSum)
maxLeftBorderSum = leftBorderSum;
}
maxRightBorderSum = 0; rightBorderSum = 0;
for (j = center + 1; j <= right; j++) {
rightBorderSum += arr[j];
if (rightBorderSum > maxRightBorderSum)
maxRightBorderSum = rightBorderSum;
}
return max(maxLeftSum, maxRightSum, maxLeftBorderSum + maxRightBorderSum);
}
int bigO_n(int arr[], int n)
{
int i, currenSum, maxSum;
currenSum = maxSum = 0;
for (i = 0; i < n; i++) {
currenSum += arr[i];
if (currenSum > maxSum)
maxSum = currenSum;
if (currenSum < 0)
currenSum = 0;
}
return maxSum;
}
int max(int a, int b, int c)
{
if (a >= b && a >= c) {
return a;
} else if (b >= a && b >= c) {
return b;
} else {
return c;
}
}
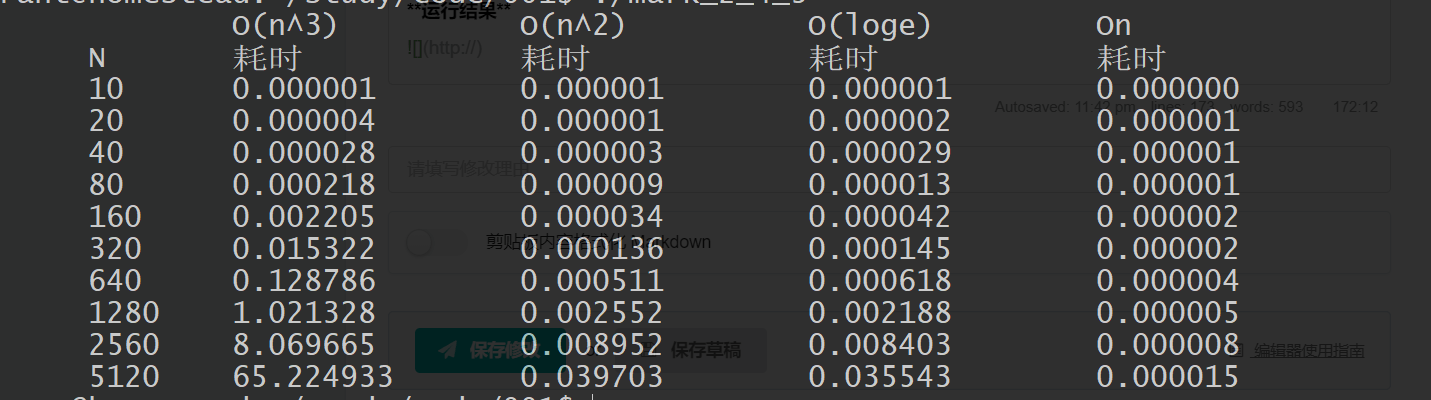
运行结果